Thesis title: Watershed Learning Merge Tree Algorithm Segments Neurons in SEM Images

1、Introduction

The automatic segmentation of neurons is a key step in the reconstruction of neural circuits based on SEM images. It is of great significance to study high-precision and high-efficiency neuron image segmentation algorithms. Based on the existing methods, this paper proposes a watershed learning merging tree algorithm to segment and identify neurons in electron microscopy images.

2、Implementation process

This method combines DCNN and watershed algorithm to segment the neuron EM images to generate superpixel images. Then the superpixel images are merged using the binary tree-based hierarchical structure to obtain the final neuron segmentation results.

3、Innovation

a).In the process of establishing a merge tree, it is necessary to determine the correlation between neighboring superpixels, so as to decide whether to generate a new parent node as a leaf node. This method computes its correlation by training a classifier, which replaces the membership function in the original method and has higher robustness.

b).In the process of parsing the merged tree, it is necessary to train the classifier to calculate the probability that the corresponding region of each tree node belongs to a single neuron. This method adds local rotation-invariant nonlinear features based on the original features and can achieve better classification results.

4、Result analysis

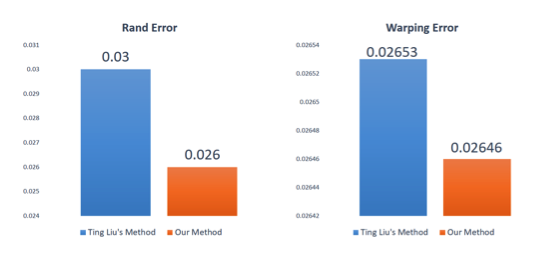
We used the Drosophila mushroom body data set to test the effect of this method. The data was obtained from the microscopic technology analysis platform of the Institute of Automation, Chinese Academy of Sciences. The image resolution is 1024*1024 and it contains a total of 1850 images with a resolution of 5*. 5*50nm/pixel. We labeled 20 of these images, using 10 as the training set and 10 as the test set. We compared the rand error and warping error with the original method. There was a slight decrease in the deformation error, and the random error decreased by 13%, Figure (a). Figure (b) is a partial segmentation result graph.

(a)